(1)最大化:max[f(c)-ac] 港口最優(yōu)裝運量發(fā)生在港口的邊際產(chǎn)量MP等于它的標準綜合單位成本a 時(shí),MP(c')=a
(2)前提分析 第一,如果港口的邊際產(chǎn)量大于a,那么在港口增加貨物運輸數量是有利的 如果港口的邊際產(chǎn)量小于a,那么減少裝運數量是有利的。 第二,我們把港口作為公共設施管理時(shí),需要達到效率。當該城市再增一標準 綜合單位商品時(shí),總產(chǎn)量會(huì )增加至: f(c+1) 那么該單位標準綜合貨物可能為城市帶來(lái)的平均收益將是: f(c+1)/(c+1) 這樣,邏輯上說(shuō),該城市每個(gè)經(jīng)營(yíng)者應該算一筆賬,就必然將每標準綜合單位 的貨物的平均收益與平均生產(chǎn)或購買(mǎi)成本相比較。
(3)如果f(c+1)/(c+1)>a,增加每標準綜合單位貨物的運量是有利可 圖的。
(4)因此,在每標準綜合單位貨物的平均利潤等于零以前,該城市應該會(huì )對港 口裝運貨物運輸作出繼續使用的選擇,并繼續增加貨物運量。
(5)但是,一個(gè)城市的所有跨境物流從業(yè)者往往是盲目的,而這種理性是做不到的! 值得思考的是,政府對港口這種公共設施的管理,以何種方式達成效率就成了必要。
簡(jiǎn)要模型分析與說(shuō)明
(1)分析過(guò)程當個(gè)人進(jìn)行成本收益分析時(shí),他所關(guān)注的是超額價(jià)值,并把價(jià) 值同成本作出比較。對他來(lái)說(shuō),這樣考慮是夠精細的,然而卻忽略了一個(gè)事實(shí),即 隨著(zhù)港口貨物運量的增加,將使港口形成堆積與擁擠,整體效率下降,可變成本提 高,這會(huì )使所有商品成本提高,從而所有商品的收益都會(huì )下降。 因為,上一階段的分析上,雖然作出的邏輯性、理性分析看似合理,但是忽略了 港口運輸行為的社會(huì )成本,即在港口堆放與運輸貨物數量太多,不僅增加每標準綜 合單位貨物的成本,也會(huì )使港口效率與貨物收益下降,無(wú)度的公共使用與放任自 流,缺乏管理,甚至可能使港口因為擁擠堆積,效率降低乃至廢棄。同時(shí),該港口城 市發(fā)展也受到影響。
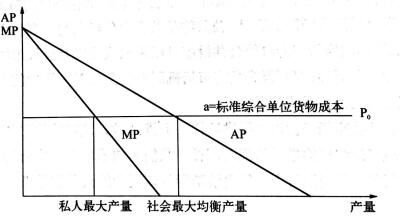
(2)邊際分析模式我們就該問(wèn)題作出邊際分析模型,以決定 最大均衡產(chǎn)量的位置。 隨著(zhù)貨物的增加,每標準綜合單位貨物的平均產(chǎn)量曲線(xiàn)呈遞減趨勢。由于平 均產(chǎn)量曲線(xiàn)呈遞減趨勢,邊際產(chǎn)量曲線(xiàn)始終位于平均產(chǎn)量曲線(xiàn)下方。


